构建和扩展决策树：实用指南

构建和扩展你的决策树：一个实践指南

解锁决策树的秘密：从基本概念到高级优化技巧和实用编码

照片由

您好，您似乎没有提供完整的句子或段落来翻译。如果您需要翻译某个特定的英文内容，请提供完整的句子或段落，我会帮您翻译成中文。

介绍

这篇文章探讨了决策树，并指导如何从头开始构建一个决策树。我将从基础开始，逐步过渡到更高级的技术来增强决策树。我将从一个简单的例子开始，来解释决策树的基础知识。然后，我将深入探讨它们背后的数学原理，涵盖熵和基尼不纯度等关键概念。我还将介绍使用逻辑函数的软决策树。在介绍完理论之后，我将深入到编码中，向您展示如何构建您的决策树，而不使用预先构建的库。最后，我将探讨优化树性能的高级技术，例如使用KS统计和结合不同的度量标准。通过本指南的结束，你将对决策树有深入的理解，并有信心构建和调整你的人工智能模型。让我们开始吧！理解基础知识与一个简单示例

让我们通过一个简单的例子来深入了解决策树的基础知识。设想我们有来自1000个人的数据显示了他们不同的年龄（我们的输入变量 x），我们想要预测他们是否就业（目标变量 Y，二元的：1代表就业，0代表未就业）。目标是构建一个模型 f(x) = Y 来预测就业状态。首先，我们需要找到最佳的截断年龄，将我们的数据分为两组：高于截断年龄的一组和低于截断年龄的一组。这种划分应该最大化两组之间就业率的差异。例如，假设30岁是最佳的分界点。这意味着30岁以上的人和30岁以下的人的就业比例显示出最大的差异。然后我们可以创建一个简单的决策规则：如果一个人的年龄大于30岁，他们更有可能被雇佣；如果他们30岁或更年轻，他们被雇佣的可能性较小。数学上，我们可以将这个决策规则表示如下：

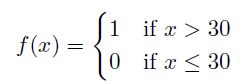
这是一个阶梯函数，其中f(x)预测1（就业）如果年龄x大于30岁，预测0（失业）如果x是30岁或更小。这个简单模型说明了决策树如何通过在最佳分割点分割数据来进行预测。实际上，决策树可以处理多个变量或一个向量：

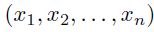
树在寻找最佳数据分割方式时会考虑不同的分割点。构建决策树的关键方面包括1）选择最佳的变量进行分割，以及2）找到最优的分割点。我将在下一段中讨论这些方面。数学概念与决策树的扩展

理解决策树

决策树是一种流行的机器学习算法，用于分类和回归任务。它们简单易懂，可以可视化，并且不需要太多的数据预处理。以下是决策树的关键概念和组成部分：

1. 基本结构

节点（Node）：决策树的基本单元，可以是内部节点或叶节点。
内部节点（Internal Node）：表示一个特征或属性。
叶节点（Leaf Node）：表示最终的决策结果或类别。

2. 构建过程

特征选择：选择最佳特征进行分割数据集。
分割数据集：根据所选特征将数据集分割成子集。
递归构建：对每个子集重复特征选择和分割过程，直到满足停止条件。

3. 停止条件

数据集为空或无法进一步分割。
达到最大树深度。
所有数据点属于同一类别。

4. 评估指标

信息增益（Information Gain）：衡量使用特征分割数据集前后信息的变化。
**基尼不纯度（Gini Impurity

让我们深入探讨决策树背后的数学原理，并研究它们如何被扩展。想象一下决策树是一系列步骤，将数据划分为不同的区域，每个区域都与不同的结果相关联。例如，在我们之前的例子中，我们使用年龄（x）来预测就业状态（Y）。我们从一个简单的决策规则开始，看起来像这样：当扩展到多个变量时，决策树模型可以表示为：

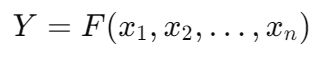
树中的每个决策节点代表基于特征 x_1, x_2, ..., x_n 的一个条件或一组条件。该模型是通过根据这些条件递归地分割数据构建的。例如，对于两个变量，年龄（x_1）和收入（x_2），一个阶梯函数可能看起来像这样：

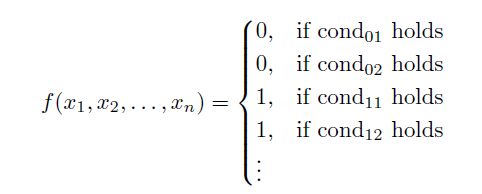
例如，如果我们有两个变量，年龄（(x_1)）和收入（(x_2)），每个变量都有其相应的截断点，决策函数会是这样的：

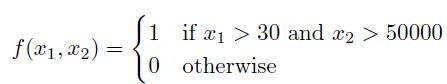
我们将使用“切树法”来解决 Y = F(x_1, x_2,…)。可以将其想象成切蛋糕。我们需要做出最好的切割，以确保每一块都有正确的成分平衡。这是它的工作原理：首先，我们确定用于分割的最重要变量。这个决定类似于选择在蛋糕上做初始切割的位置。分割应该基于年龄、收入还是其他因素？杂质度量

这涉及到根据熵、基尼不纯度和信息增益等标准选择最佳变量和最优分割点。熵是衡量数据中不纯度或随机性的指标，计算公式为：

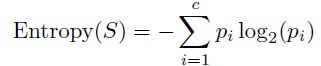
这里 S 表示数据集，c 表示类别的数量，而 p_i 表示类别 i 中实例的比例。设想我们将数据进行分割，使每个组尽可能纯净。熵度量了随机性或不纯度。熵越低意味着组越纯净。 基尼不纯度是另一种衡量不纯度的方法，其公式如下：

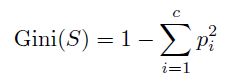
这是另一种衡量纯度的方法，计算如果你从一组中随机挑选，你随机挑选错误物品的频率。Gini不纯度越低意味着错误越少。 信息增益衡量的是在分裂后熵或杂质的减少：

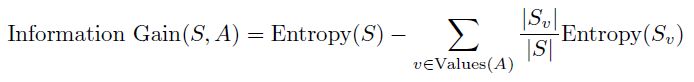
这告诉我们在分割后数据的纯度提高了多少。它衡量的是熵的减少。较高的信息增益意味着我们进行了一个好的分割。这些指标很重要，因为它们帮助树确定最佳的分裂点，确保每次分裂都使各组尽可能相似。例如，如果你根据年龄和收入预测人们是否会购买产品，你希望创建的组别中，人们更有可能做出相似的决策。你可能会质疑如何在实践中使用这些不纯度度量。别担心，我已经为你准备好了。以下是根据我的经验和研究的总结：

选择适当的不纯度度量：根据你的数据集和问题类型，选择最适合的不纯度度量。例如，对于二元分类问题，可以使用信息增益或基尼不纯度。
理解不纯度度量的含义：了解每种不纯度度量的含义和计算方式，以便更好地解释决策树的结果。
使用不纯度度量构建决策树：在构建决策树时，使用所选的不纯度度量来确定最佳的分割点。
评估模型性能：使用不纯度度量来评估决策树模型的性能，并通过调整模型参数来优化性能。
比较不同不纯度度量：在实践中，比较不同不纯度度量的效果，以确定哪种度量最适合你的特定问题。
结合业务知识：在应用不纯度度量时，结合业务知识和领域专家的意见，以确保模型的决策与实际业务目标一致。
注意过拟合：在使用不纯度度量

何时使用每个标准？ 熵：将熵想象为一个一丝不苟的组织者。当你想要精确地了解你的群体混合程度时，请使用它。它非常适合那些你关心类别确切分布的任务。 基尼不纯度： 基尼是您快速、可靠结果的首选。它在不需要太多麻烦的情况下为您提供了良好的纯度度量。在解决二元分类问题时，它在计算上不那么繁重，并且能够高效地完成工作。 信息增益：当使用诸如ID3、C4.5或C5.0等算法时，请使用此度量，因为它是关于理解每个分割对您有多大帮助的。它也适用于观察决策树中每个决策的附加价值。平滑函数用于软树

一个自然的问题是：是否存在任何平滑的步函数用于“剪枝法”？

这对于神经网络来说非常重要，因为传统的决策树是非可微的阶梯函数，在训练神经网络模型时存在困难。在神经网络中使用平滑的软树状函数作为激活函数将能够实现反向传播和梯度下降。此外，平滑的软树可以通过提供概率输出来促进训练并提高性能。“软”通过平滑决策边界来防止过拟合，从而创建一个更稳定和可泛化的模型。为了引入软树的概念，我们可以使用逻辑函数来平滑阶梯函数。逻辑函数定义为：

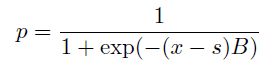
其中 s 是截断点，B 是一个较大的正值（惩罚项），定义了函数的陡峭程度。当 B 较大时，这个函数近似于一个阶梯函数，因为上述方程对于 xs 快速接近 1。这允许我们为树的分支分配概率，有效地从软决策树过渡到硬决策树。将此纳入我们的树中，预测函数可以更新如下：

如果选择了“软”，则预测基于p和硬树分配的加权平均值。这种方法引入了软树的概念，其中决策边界是平滑的而不是尖锐的。在统计学和机器学习中，杂质度量是用来评估分类问题中数据集的纯度。以下是一些常见的杂质度量及其相互之间的关系：

熵（Entropy）：熵是衡量数据集中类别分布的不确定性的度量。熵越高，数据集的纯度越低。熵的计算公式为： [ H(S) = -sum_{i=1}^{n} p_i log_2 p_i ] 其中，( p_i ) 是数据集中第 ( i ) 类的比例。
信息增益（Information Gain）：信息增益是熵的减少量，用于评估特征对数据集纯度的影响。信息增益的计算公式为： [ IG(S, A) = H(S) - sum_{j=1}^{m} frac{|S_j|}{|S|} H(S_j) ] 其中，( S ) 是数据集，( A ) 是特征，( S_j ) 是基于特征 ( A ) 的第 ( j )

让我们来探讨软树函数与硬树的不纯度度量之间的关系。在逻辑回归中，正类的概率是使用逻辑函数来建模的：

给定这个模型，单个数据点 (x, y) 的似然函数是：

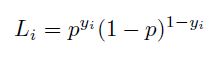
数据集的整体可能性是：

取对数，我们得到对数似然函数：

从逻辑函数中代入p：

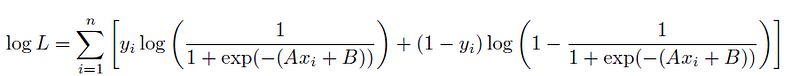
这表明，在逻辑回归中最大化似然函数的目的是找到最佳的系数A和B，以有效地分离类别。这类似于在基尼或熵项中找到最小化杂质的分割。我们首先比较逻辑回归似然和基尼不纯度：

如果数据是完全分离的，逻辑回归模型的决策边界将最小化重叠，从而产生纯净的子集（低基尼不纯度）。当p接近0或1（纯净类别）时，基尼不纯度2p(1-p)接近0，表示纯净节点。然后我们比较逻辑回归似然和熵：对数似然函数包含项 −p log(p) − (1 − p) log(1 − p)，类似于熵公式。这意味着通过最大化对数似然，我们也在减少熵。我们的目标是获得有信心的分类，其中 p 接近0或1。当 p 接近0或1时，熵 −p log(p) − (1 − p) log(1 − p) 变为0，表示纯节点。理解和实现具有逻辑函数的软树方法在深度学习和Kolmogorov-Arnold网络（KAN）中也很重要，因为它弥合了决策树和神经网络架构之间的差距，使模型更加灵活和强大。在下一节中，我将讨论传统决策树的代码实现。这可以为您提供对它们机制的清晰理解。此外，它还将帮助读者开发他们的树并理解模型的工作原理。我还将展示为什么使用对数函数的参数化方法很重要。实现一个传统的决策树从零开始

决策树是一种流行的机器学习算法，用于分类和回归任务。它们易于理解和实现，并且可以处理数值和类别数据。在本文中，我们将逐步介绍如何从零开始实现一个传统的决策树算法。

1. 理解决策树的基本概念

决策树通过一系列的问题将数据分割成不同的分支，直到达到一个叶节点，该叶节点代表一个预测结果。这个过程基于特征选择和分割点，以最小化数据的不纯度。

2. 计算不纯度

不纯度是衡量数据集中类别分布的混乱程度的指标。常见的不纯度度量方法有：

Gini不纯度：计算每个类别的比例的平方和的补数。
熵：计算每个类别的概率的负对数之和。

3. 特征选择

特征选择是选择最佳特征进行分割的过程。这可以通过计算每个特征的不纯度减少量来实现，然后选择减少量最大的特征。

4. 递归分割

使用特征选择的结果，对数据集进行分割，然后对每个子集递归地应用

我将学习从头开始构建决策树分类器的代码，不依赖于像scikit-learn这样的预构建库。这种动手方法将帮助您理解决策树的底层机制以及如何自己实现它们。让我们逐块深入代码，重点关注树生长和最佳分割计算的关键部分和更复杂的方面。 基尼不纯度计算 def gini_impurity(y): m = len(y) return 1.0 - sum((np.sum(y == c) / m) ** 2 for c in np.unique(y))

该函数计算给定标签集y的基尼不纯度。在这里，我们使用这个度量来搜索分割点。 寻找最佳分割点 ``` def best_split(X, y): best_gini = 1.0 best_idx, best_thr = None, None m, n = X.shape

for idx in range(n):
    thresholds = np.unique(X[:, idx])
    for thr in thresholds:
        left_mask = X[:, idx] < thr
        right_mask = ~left_mask
        if sum(left_mask) == 0 or sum(right_mask) == 0:
            continue

        gini = (sum(left_mask) * gini_impurity(y[left_mask]) +
                sum(right_mask) * gini_impurity(y[right_mask])) / m

        if gini < best_gini:
            best_gini = gini
            best_idx = idx
            best_thr = thr

return best_idx, best_thr

```

该函数通过最小化基尼不纯度来寻找最佳特征和分割数据的阈值。以下是其过程的详细分解：

初始化：首先，函数会初始化一个空列表，用于存储分割点和相应的基尼不纯度。
遍历每个特征：对于数据集中的每个特征，函数会遍历该特征的所有可能值。
计算基尼不纯度：对于每个特征值，函数会计算在该特征值处分割数据的基尼不纯度。基尼不纯度是衡量数据集纯度的一种指标，其值越小表示数据集越纯。
更新最佳分割点：如果当前计算的基尼不纯度小于之前记录的最小基尼不纯度，则更新最佳分割点和相应的基尼不纯度。
选择最佳特征和阈值：在遍历完所有特征的所有可能值后，函数会选择具有最小基尼不纯度的特征和对应的阈值作为最佳分割点。
返回结果：最后，函数返回最佳特征、最佳阈值以及在该分割点处的基尼不纯
初始化：best_gini 被初始化为 1.0，代表最差的不纯度。best_idx 和 best_thr 将存储用于分割的最佳特征索引和阈值。
遍历特征和阈值：该函数遍历每个特征以及该特征的每个唯一阈值。对于每种组合：
掩码：它创建掩码以根据特征值是否低于或高于阈值，将数据分割成左和右的子集。
基尼计算：通过将左和右子集的基尼不纯度按其大小加权，计算分裂的基尼不纯度。 更新最佳分割点 如果当前分裂的基尼不纯度低于迄今为止观察到的最佳值，该函数将更新best_gini、best_idx和best_thr。 class Node: def __init__(self, gini, num_samples, num_samples_per_class, predicted_class): self.gini = gini self.num_samples = num_samples self.num_samples_per_class = num_samples_per_class self.predicted_class = predicted_class self.feature_index = 0 self.threshold = 0 self.left = None self.right = None

该类表示决策树中的一个节点。它存储了： * 基尼系数：节点的基尼不纯度。 * num_samples: 节点处的样本数量。 * num_samples_per_class: 每个类别的样本分布。 * 预测类别：节点处的类别预测。 * 特征索引和阈值：用于存储分割的最佳特征和阈值。 * 左指针和右指针：指向左右子节点的指针。 决策树分类器 ``` class DecisionTreeClassifier(BaseEstimator, ClassifierMixin): def init(self, max_depth=None): self.max_depth = max_depth

def fit(self, X, y):
    # Check for NaN or infinite values in the data
    if np.any(np.isnan(X)) or np.any(np.isnan(y)):
        raise ValueError("Input data contains NaN values.")
    if np.any(np.isinf(X)) or np.any(np.isinf(y)):
        raise ValueError("Input data contains infinite values.")

    self.classes_ = np.unique(y)
    self.n_classes_ = len(self.classes_)
    self.n_features_ = X.shape[1]
    self.tree_ = self._grow_tree(X, y)
    return self

```

我们的决策树的主要类。它继承自 BaseEstimator 和 ClassifierMixin 确保与 scikit-learn 的兼容性。以下是每个方法的作用：

BaseEstimator 是 scikit-learn 中所有估计器的基类，提供了一些基本方法，如 get_params 和 set_params，用于获取和设置估计器的参数。它还定义了一些其他方法，如 fit、predict、transform 和 score，这些方法在 scikit-learn 中的大多数估计器中都有实现。
ClassifierMixin 是 scikit-learn 中的一个混入类，它提供了一些分类器特有的方法，如 score 和 predict_proba。score 方法用于评估分类器的性能，predict_proba 方法用于预测每个类别的概率。

这两个类通常一起使用，以确保自定义的估计器或分类器与 scikit-learn 的其他组件兼容。通过继承 BaseEstimator 和 ClassifierMixin，你可以确保你的自定义类具有 scikit-learn 期望的方法和属性。 * 初始化：设置树的最大深度。 * 模型拟合：检查输入数据中的NaN或无限值，初始化类别和特征信息，并开始树生长过程。 培育树木 ``` def grow_tree(self, X, y, depth=0): num_samples_per_class = [np.sum(y == i) for i in range(self.n_classes)] predicted_class = np.argmax(num_samples_per_class) node = Node( gini=gini_impurity(y), num_samples=X.shape[0], num_samples_per_class=num_samples_per_class, predicted_class=predicted_class, )

if depth < self.max_depth:
    idx, thr = best_split(X, y)
    if idx is not None:
        indices_left = X[:, idx] < thr
        X_left, y_left = X[indices_left], y[indices_left]
        X_right, y_right = X[~indices_left], y[~indices_left]
        node.feature_index = idx
        node.threshold = thr
        node.left = self._grow_tree(X_left, y_left, depth + 1)
        node.right = self._grow_tree(X_right, y_right, depth + 1)

return node

```

该方法递归地构建决策树： 1. 节点创建：使用基尼不纯度、样本计数和预测类别初始化一个新节点。 2. 分裂节点：如果当前深度小于最大深度max_depth，它将找到最佳分裂点。如果找到了有效的分裂点： * 左右子集：根据分割创建数据的子集。 * 递归调用：递归地增长左子树和右子树。 进行预测 ``` def predict(self, X): return np.array([self._predict(inputs) for inputs in X])

def predict(self, inputs): node = self.tree while node.left: if inputs[node.feature_index] < node.threshold: node = node.left else: node = node.right return node.predicted_class ```

预测方法使用辅助函数 _predict 从根节点遍历到叶节点，为每个输入进行预测： 1. 遍历树：从根节点开始，根据特征值和阈值，它向左或右子节点移动。 2. 叶节点：一旦到达叶节点，它将返回存储在叶节点的预测类别。这种定制实现的决策树分类器提供了对决策树工作原理的全面理解。有了这些知识，您可以在机器学习算法中处理更高级的应用和定制。构建我的决策树与增强的分裂标准

在本节中，我将展示一种扩展的决策树方法，该方法结合了Kolmogorov-Smirnov（KS）统计量、熵以及两者的组合来确定最佳分割点。此外，我们将引入一个“软”决策树因子，使用逻辑函数：

```markdown

扩展决策树方法

KS统计量

KS统计量是一种用于测量两个概率分布之间差异的非参数方法。在决策树中，我们可以使用KS统计量来评估特征值的分割点。

熵

熵是信息论中的一个概念，用于衡量数据的不确定性。在决策树中，熵可以帮助我们评估分割后的数据集的纯度。

KS统计量与熵的组合

结合KS统计量和熵，我们可以更全面地评估分割点的质量。

软决策树因子

使用逻辑函数作为软决策树因子，可以增加模型的灵活性。逻辑函数通常定义为： [ ext{Logistic Function} = frac{1}{1 + e^{-x}} ] 其中，( x ) 是输入值。

决策

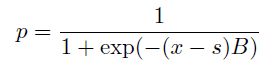
为分支分配概率，使决策树更加适应性强和稳健。为什么使用KS？

KS统计量衡量两个样本累积分布之间的最大差异，因此，在本文中，我将使用它来识别最显著的分割点。

传统上，Kolmogorov-Smirnov（KS）统计量用于检验两个样本是否来自同一分布的假设。它测量两个样本的经验累积分布函数（CDFs）之间的最大距离。在数学上，两个样本F_1(x)和F_2(x)的KS统计量定义为：

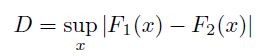
这种方法也已被证明在区分两个类别方面是有效的。因此，我将其作为一个有用的工具用于决策树。代码的关键部分

让我们更仔细地看看代码的关键部分： 1. 初始化：该类使用诸如深度、每个分割的最小样本数、潜在切点数量、分割标准以及是否使用“软”树选项等参数进行初始化。 class DecisionTree(BaseEstimator, ClassifierMixin): def __init__(self, depth=10, min_samples_split=2, num_cut_points=100, split_way='entropy', soft=False, B=5): self.depth = depth self.min_samples_split = min_samples_split self.num_cut_points = num_cut_points self.split_way = split_way self.soft = soft self.B = B self.tree = None

构建树：该方法递归地构建树。它根据_best_split方法确定的最佳分割点将数据分割为左和右子集。如果达到最大深度或样本数量低于最小值，则创建叶节点。 def _build_tree(self, X, y, depth): if depth == 0 or len(X) < self.min_samples_split: return self._leaf_value(y) feat_idx, threshold = self._best_split(X, y) if feat_idx is None: return self._leaf_value(y) left_idx = X[:, feat_idx] < threshold right_idx = ~left_idx left_tree = self._build_tree(X[left_idx], y[left_idx], depth-1) right_tree = self._build_tree(X[right_idx], y[right_idx], depth-1) return (feat_idx, threshold, left_tree, right_tree)

寻找最佳分割点：_best_split方法使用KS统计量、熵或两者来评估潜在的分割点。它遍历每个特征的阈值，并计算左右分割之间的KS统计量和熵。选择得分最高的分割点。 ``` def _best_split(self, X, y): best_score = -np.inf split_idx, split_thresh = None, None for feat_idx in range(X.shape[1]): thresholds = np.linspace(np.min(X[:, feat_idx]), np.max(X[:, feat_idx]), self.num_cut_points) for threshold in thresholds: left_idx = X[:, feat_idx] < threshold right_idx = ~left_idx if sum(left_idx) == 0 or sum(right_idx) == 0: continue

        if self.split_way == 'KS':
            ks_stat, _ = ks_2samp(y[left_idx], y[right_idx])
            score = ks_stat
        elif self.split_way == 'entropy':
            left_entropy = entropy(np.bincount(y[left_idx], minlength=self.n_classes_) + 1e-10)
            right_entropy = entropy(np.bincount(y[right_idx], minlength=self.n_classes_) + 1e-10)
            total_entropy = (sum(left_idx) * left_entropy + sum(right_idx) * right_entropy) / len(y)
            info_gain = entropy(np.bincount(y, minlength=self.n_classes_)) - total_entropy
            score = info_gain
        elif self.split_way == 'both':
            ks_stat, _ = ks_2samp(y[left_idx], y[right_idx])
            left_entropy = entropy(np.bincount(y[left_idx], minlength=self.n_classes_) + 1e-10)
            right_entropy = entropy(np.bincount(y[right_idx], minlength=self.n_classes_) + 1e-10)
            total_entropy = (sum(left_idx) * left_entropy + sum(right_idx) * right_entropy) / len(y)
            info_gain = entropy(np.bincount(y, minlength=self.n_classes_)) - total_entropy
            score = (ks_stat + info_gain) / 2
        else:
            raise ValueError(f"Unknown split_way: {self.split_way}")

        if score > best_score:
            best_score = score
            split_idx = feat_idx
            split_thresh = threshold

return split_idx, split_thresh

```

使用“软”树进行预测：predict_proba 方法使用逻辑函数为每个分支分配概率。这使得树变得“软”，能够更好地处理不确定性。 ``` def _predict_proba(self, inputs, tree): if not isinstance(tree, tuple): return np.eye(self.n_classes)[tree] feat_idx, threshold, left_tree, right_tree = tree

prob = 1 / (1 + np.exp((inputs[feat_idx] - threshold) * self.B))
left_prob = self._predict_proba(inputs, left_tree)
right_prob = self._predict_proba(inputs, right_tree)

combined_prob = prob * left_prob + (1 - prob) * right_prob
combined_prob /= combined_prob.sum()

return combined_prob

```

这里是结果：

结果显示，KS统计量可以提升决策树的性能。虽然软树并没有提高性能，但它有助于理解如何将概率赋值整合到决策树中。这种方法对于神经网络很有用，其中平滑的激活函数对于反向传播和梯度下降非常重要。软树方法增加了机器学习模型的灵活性和进一步优化的潜力。结论

我编写了这份指南，因为决策树是机器学习方法中的重要工具，如XGBoost、LightGBM和神经网络。虽然人们经常使用像scikit-learn这样的预构建包，但理解决策树的基本机制和数学原理可以促进改进和新算法的创造。通过从头构建决策树，你将学习如何决定分割点，如何通过不纯度度量指导这些分割，以及KS统计量如何提高性能。我还介绍了软树的概念，这对于整合概率很有用，并且对神经网络很重要。掌握决策树的基础知识有助于您为特定任务微调和优化模型。它还有助于在机器学习项目中构建高级应用程序和自定义功能。 Python 脚本可以在我 GitHub 仓库中找到：

GitHub — datalev001/decsiontree

由于您提供的文本只有一个点（.），这在Markdown中通常表示一个列表项或者是一个句子的结束。然而，由于没有更多的上下文，很难提供一个准确的翻译。如果您能提供更多的信息或完整的句子，我将能够为您提供一个更准确的翻译。